
「えっ!?」と私を混乱させまくってくるぜ~
解説を聴いても「エッ!?」の連続や~
物体の温度と光のスペクトルの関係を知るために
「黒体放射のスペクトル」を実際に調べた結果
⇓
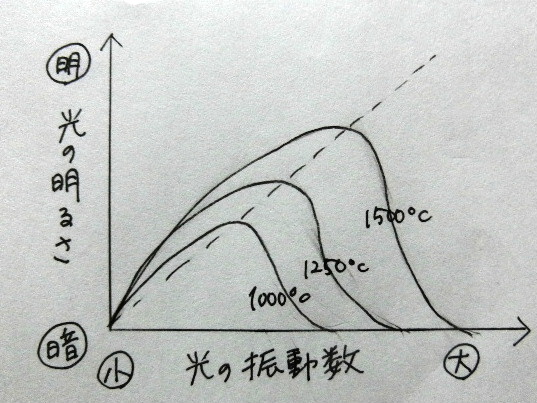
こういった分布線になることがわかった。
或る点を頂点として、ストンと下がるのだ。
私場合は、このストンと下がりきった「振動数が大で光がほぼゼロ」状態の先にあるモノが気になったが当時の研究者達はもっと違う点で驚いていたようです。
プランクが研究していた19世紀当時の物理学では
理論上「スペクトル分布線は右肩あがり(っぱなし)」になると予測されてた、と。
⇓
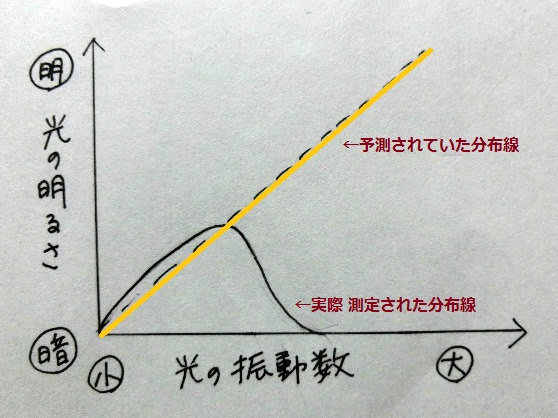
私としては、あまりにも数学的世界過ぎて
「有限の実世界」において不気味にして単純すぎるんじゃね!?とも思ったこの予測…
我が量子論の旅ガイドこちらで、優しく解説してくれておりますが
筆者の教授の予測に反して「無知度がハイレベル」な私は「???」の渦の中へ
⇓
私なりにザックリ解説しますと
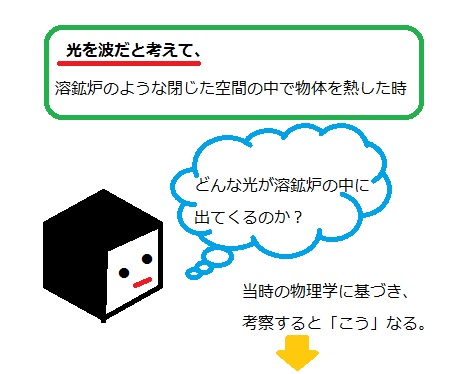
”振動数が大きな光ほど、その明るさ(強度)がどんどん増していく”
しかも!振動数の大きな光を「いくらでも」考えることが可能な為、
その分布線は右肩上がりっぱなしになってしまう、というのです。
んん!? えっ!?
光が電磁波の一種とマクスウェルが予言して、ヘルツが電磁波の存在を証明したのが…
1864年~1888年と19世紀後半で、プランクがエネルギー量子仮説を唱えたのが1900年12月だから…
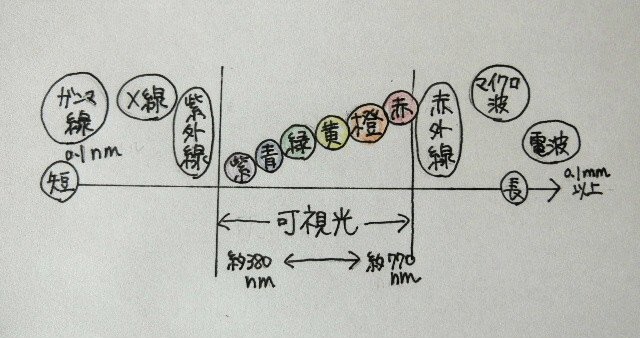
その当時は電磁波の中でも「可視光」は一部という認識はまだなかったのかな?
でも、でもX線は1895年に発見されてるみたいだし…無知な私の脳は大渋滞中さ~
大混乱中ですが、「こう予測される理由」というのを
「量子論」を楽しむ本 ミクロの世界から宇宙まで最先端物理学が図解でわかる! (PHP文庫)
の中で佐藤教授が優しく教えてくれております。
①溶鉱炉の中で温度が安定した時、その中に存在する光の波長の中で一番大きいのもは溶鉱炉の大きさの2倍のものとなる。そして、それより小さな波長の光(=振動数が大きな光)は無限に想定することが可能である。
②熱力学には「エネルギーの等分配の法則」というものがあり、これによると温度が安定した溶鉱炉内の光には どの光の波1個(振動1個)にも同じ量のエネルギーが配られることになる。
③そうすると、波長が短い光 つまり振動数が大きな光ほど、その振動数に応じて大きなエネルギーを持つはずである。
ということになり、スペクトル分布線は右肩上がりの線になるのです。
※p54より
無知な私からすると①の「その中に存在する光の波長の中で一番大きなものは溶鉱炉の大きさの2倍のものとなる」の時点で「えっ!? どうやって光として存在できんの??」と脳みそ沸騰中でチンプンカンプンす。
②の話しからするに炉の中で「波1個」にも成れないのに、光として存在はしてるんか?どうやってエネルギーもらってるんや~、と。
それよりも何よりも
「炉内のエネルギーは有限じゃね!?」って引っかかりますよね、ねっ!
こうして「???」だらけの疑問と違和感の渦にのまれつつ
私の量子論への寄り道旅は続いていきます。


