
どうなってるんだ、今度は「気体が放つ光の線スペクトル」だと⁉
なんで皆、光に夢中なんや!? トートも光を目指せって云うてたしなぁ…
無知な私に量子論の世界を優しく案内してくれる1冊
今日からは、ボーアが如何にして「水素原子のバルマー系列関数式」から
ボーア原子モデル完成までに至ったかを追っていく~
つーことで閃きの素となった「バルマーの発見」から見ていこう☆
ちなみに、バルマーはスイスの中学校の数学教師だったんだよ!
その前に、「水素原子のスペクトル」とは何か?をおさえておこう。
真空にしたガラス管の中に微量の気体を入れ⇒放電すると
”気体の種類(原子の種類)毎に特有の光を放つ”
↓
この光を分光器に通してスペクトルを分析する研究が19世紀の中ごろから行なわれてたんだって。皆、光、スペクトル好きなんやなぁ…光を追ってしまうんやな。
「黒体放射のスペクトル」って見てきたでしょ、
この場合、様々な波長の光を連続的に含んでいるため、その光をプリズムに通すと波長ごとに分かれた光は「帯状に広がる」=これを連続スペクトルっていうんや
たぶん、連続スペクトルのイメージはこれでいいんやと思う。
↓
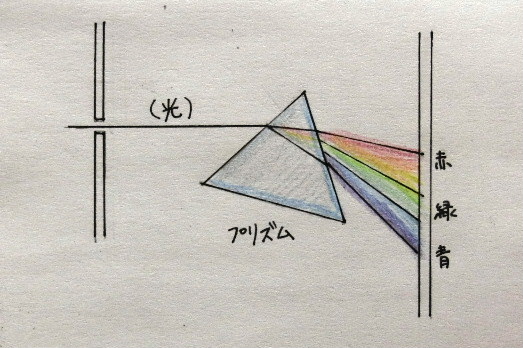
「気体が放つ光をプリズムに通すと」ちがったスペクトルになるんや!
帯状に広がる「連続スペクトル」ではなく、細い線状の光がところどころに現れる「線スペクトル」になるんですって。
↓
線スペクトルが意味することというのは
”連続的ではなく、とびとびの波長の光だけを含んでいる”ということ。
でた!「とびとびの~」というイレギュラー
んでな、プランクが「とびとびの変化」から量子というアイディアとプランク定数を導きだしたように 水素原子のスペクトルを見てその法則性を解き明かした人物が登場するんや!⇒それが数学教師だったバルマーなんです(^^)
このバルマーの発見が凄いんです。
なんでこんな数値から、ここまでのもの見える(見つけ出せる)んや!?
と私は驚愕しっぱなしっす。数学者の思考、怖えぇっ
(つづく)




