
「何でかな?」と深く考えてみる…そんな思考の癖をつけたいもんだね~
電子に限らず、”すべての物質は(↓)の式でもとめられる波長をもつ波である”
と考え、「物質波」と名付けたド・ブロイ君。

これって「すべての物質は運動によって波動性をもつ」と解釈していいのかな?
この宇宙に存在してるってことは、そもそも「運動中」だから…存在するすべてのモノは波動性をもつと解釈していいのか?
地球も太陽系も銀河系も皆 動き続けているので
その中にいる我々も必然的に「動き続けている」わけですよね?
まーこの辺のこと一旦おいといて、
ド・ブロイ君に「電子の波」どう見えていたのかを覗いていきましょう~
無知な私に量子論の世界を優しく案内してくれる良書がこちら
↓
そもそも物理が示す「波」とは
”ある一点に存在するものではなく、ある広がりをもって存在している”
↓
原子の中の電子波も原子核の周囲に広がっている ことになる
そこでド・ブロイ君はこう考えたのです。

一周してきた波の山と山が重ならないと干渉により波は消えてしまう…のだから

※私のフリーハンドの技量不足でガタガタですが同じ波長の波っす(--;
「一周してきた波の山と山がピッタリと重なると波は存在し続ける」
この時、電子の波の「一周の長さ」は”必ず” 波長×整数倍になっている わけです。
ボーアの量子条件の式を思い出してほしい。

原子内の電子はどこにいてもいいのではなく、決められた円軌道上だけを動いている。
その軌道半径は「ある条件(=ボーアの量子条件)」にあうとびとびの値のものだけになる。
この「ある条件」を示す「ぼあーの量子条件の式」とは
↓
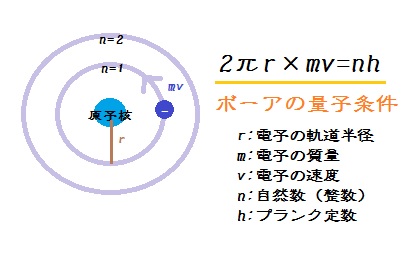
ここに「とびとびの値をとる」その基たる「整数倍を示す=n」があり、
ド・ブロイが唱える電子の波と繋がりが見えてきた~!
電子を「波」と考えた場合、
”電子の波が原子核の周囲に存在する条件にも「整数(n)倍」という条件が付く”
ドブロイ君はボーアの量子条件との「この共通点」に注目し、
電子の波×ボーアの量子条件を見事に融合させた式を示したのです。
やはり「この世の法則(性)」とは数式で示せるんやな~(感慨深い)
私という生命も実にシンプルな法則(数式)で生き・生かされているのかも。
んでな、前回「プランク定数h」の(この世界における)支配力に震えた私ですが
縄文の数学を覗くと この「h」が示す実際の数字の重要性に縄文人が既に気づいていたかもしれないんですよ…その点に更に震え倍増した。
つづく。




