
比較の結果を表現する必要性から「第三の点」が生みだされました。
3つの点がつくる幾何学図形「三角形」
1の・(点)、2のー(直線)と違い一気に「物」「形」が出現した感じしませんか?
私が世界・自然界・宇宙の法則を探る為に
幾何学模様に注目し、今手元に教科書として置き読み込んでいる1冊
⇓
「2」で2つの点がつくる直線=一次元でしたよね。
では「3」は「2」からどう変化を起こしたのでしょうか?
3つの点がつくる三角形は二次元空間を定義する

3つの点からつくられる「三角形」
3を象徴する図形といってポン!と頭に浮かぶのも「三角形」ですよね。
- 「1」は無限の速度で動き回る「・」点
- 「2」は2つの点を通る「ー」直線
- 「3」は3つの点から作られる「△」三角形
私たちが普段「図形」として認識するのって
三角形からではないでしょうか?
(※点も直線も図形といえば図形の一種ですけど)
図形=物=存在がわかりやすく認識されるのが「3」からではないかしら(^^)
それは何でかというと
3つ点があると、
ある1つの平面を定めることができ、
従って3つの点により
2次元空間が定義されます。
まさに「ここ」ですよね。
2つの点がつくる1次元から3つの点がつくる2次元空間へ
「平面」「面」が現れ認識できるようになったのです。
◆物質世界への産声
ここで1つ注意しなければいけないことは、
先ほど私の認識イメージで
”1つの点からはじまり3つの点で「三角形」が出現し
図形=物=存在の認識がしやすくなった”
と言っちゃいましたが
⇓
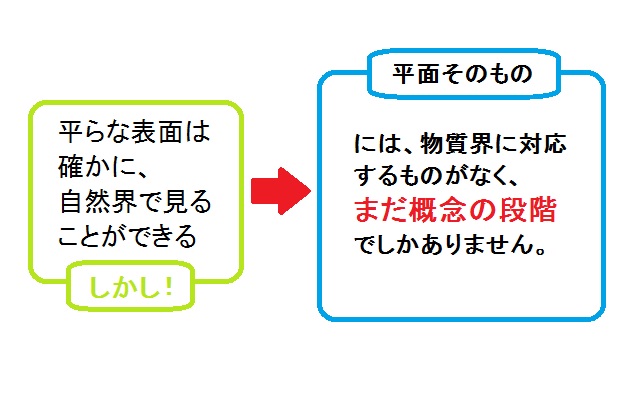
この辺をごっちゃに平気でしちゃう私(^^;)
でも、そうそう、これ重要ですよね。
3つの点がつくる三角形、その出現により平面が定められ
2次元空間が定義されますが
ここで表れた「平面そのもの」は”まだ概念の段階”でしかない…
けど、だんだんと物質世界誕生の産声が聞こえてきませんか?
3が1の創造に大きな役割を担っているのです。
なかなか壮大な話になっていくので
次回からはより気合を入れて紹介していきます。
少しずつ、<創造活動>にある法則が見えてきた気がする~楽しい☆
つづく


