【量子論への寄り道】67:ボルン君の「波動関数Ψの確率解釈」

『波動関数Ψの絶対値の二乗したもの』が電子の発見確率と

どのように関係してるか？ 追ってみる～

無知な私に量子論の世界を優しく案内してくれる良書

「量子論」を楽しむ本 ミクロの世界から宇宙まで最先端物理学が図解でわかる！ (PHP文庫)

ボルン君が唱えた説によると

”波動関数Ψの絶対値の二乗が電子を発見する確率を表す”

”波動関数Ψの絶対値を二乗した値は 電子がその場所で発見される確立に比例する”

ということですが、これはどういったことなのか？

「絶対値」なんで正の実数になりますよね。

（故に二乗しても正の実数となる）

では佐藤先生が先に紹介した本のなかで示してくれた、波動関数Ψ（複素数の波）の「実数部分だけ」（or虚数部分だけ）を取り出し描いた図をご覧ください。

⇓

縦軸と横軸が何を示すかをしっかりおさえて～

パッと見ただけでも「ｂ地点で電子が発見される確率が一番高いな」ってことはわかる。

⇓

でも「a」地点や他の地点と比べて、どれほどその確率が高いのかがイマイチわからんじゃろ。そこでボルン君のアイディアが役立つんや～

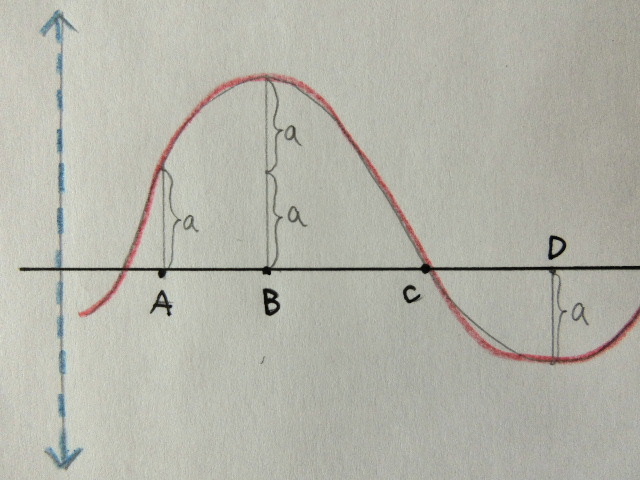
振幅＝波動関数Ψの大きさ、なのでそれぞれの地点の振幅を

「Ａ点の振幅＝a(1a)」として絶対値の比でみていこう！

• Ａ点の振幅「1a」
• Ｂ点の振幅「2a」
• Ｃ点の振幅「0」
• Ｄ点の振幅「1a」

この時、電子が「Ｂ点」で発見される確率は「Ａ点」に於いて発見される確率の「4倍」になってる、ということをボルン君は教えてくれているのだ。

Ａ点の振幅：Ｂ点の振幅＝１：２

故にＢ点で電子が発見される確率はＡ点で発見される確率の「２の二乗」倍ってことになるわけや～

ボルン君が教えてくれんかったら、無知な私はこの波図をみただけ即「Ｂ点の発見確率はＡ点の2倍や」と思い込んでしまうとこやった～あぶねぇ～（感覚だけで生きてます）

ってことは「Ｄ点」と「Ａ点」の発見確率は同じやな。

でも気になるのは「Ｃ点」の「確率0」ですよね～

どこで電子が発見されるかは「100％ここ」とはいえないのに

絶対に「ここで発見されることは無い」といえる場所はあるのか～興味深い。

ま～これはΨの実数部分だけ（or虚数部分だけ）を取り出して無理くり

電子の波を表現したものだから 電子の波の全体像ではないわけだけども。

”Ψの絶対値が大きい場合ほど、そこに電子を見つける可能性が高くなる”

ってことがわかっただけでもすごいし「Ψの絶対値の二乗の値」によって

確率比が掴めるってことだから、だんだん「電子の波」の姿をつかみかけてる感はあるよね。

ここから電子が持つ「i（虚数）」性質に迫っていくよ～

カム界や縄文の数学に繋がる部分にはいていくで～

（つづく）

にほんブログ村

クイズで学ぶ大学の物理　たいくつな力学と波動がおもしろい (ブルーバックス)

物理の完全制覇 プラチナ例題[力学・熱・波動編]

波動の法則