
よーし、やっと「2」に関する「幾何学図形」に話は進むよ~
「2」が象徴する世界を覗いたら
形で追っていきましょう☆
BBAが「この世界の法則」解明に参考にしている1冊
⇓
2つの点が創りだす「直線」
1を象徴する図形が「点」と「円」
点こそ「創造」の中心ではじまりでしたよね。
<絶対なるもの>の創造原理<一なるもの>を象徴する「点」は
無限の速度であらゆるところを動き回る「・」でしたよね。
1が2を生み出す
⇒1から生み出された「2つのモノ」=「2つの点」

これがどんな幾何学図形をつくるかというと
「2つの点」だけでも図形ですが
1から生まれたモノは「関係性」を濃く持っていましたよね。
⇓
そんで、私たちが本能的に持つ感覚的にも
2つの点から図形を描こうとすると、自然とこうなるのではないでしょうか?

※これはわかりやすく「・」を大きく誇張してあります
両極にある2つのモノ⇒「対立する2者」をよく表現できてますよね(^^)
2つの点から1本の直線(図)ができるのです。
更に2つの点がつくる直線はもう1つの姿があります。
2つの点を通る無限に伸びる直線
先ほど私が2点を結んだ線は「点と点を結んだもの」でしたが
2つの点がつくる図形を考える時「2つの点を通るもの」という考えもできる。
⇓
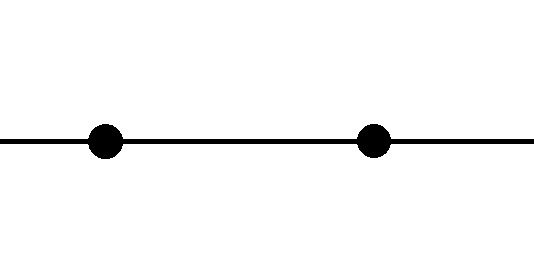
※2つの点をわかりやすく誇張してます
1は自分の存在を認識するために「2」を生み出し、
「2」は1ににとって自分を見るための鏡でしたよね。
1から生まれた2は「1」性質を濃く受け継いでいるので
2つの点がつくる図形も「点がつくる円」に似た性質を持っています。
神とは円であり、その中心はあらゆる場所に存在し、
円周はどこにもない
また<1なる点>は円を創造した時
その姿を消してましたよね。
円を描くとき「中心点」を必要としますが
完成した円にはその点が消えてる。
これと同じことが「2つの点を通る直線」にもいえるのです。
⇓
はじめに2つの点だけがあり、
その2つの点を通る線を引いた途端に2つの点は姿を消す。
直線は無限に長く伸びており、
私たちはその無限の全体を描くことができない。
私たちはその一部しか描くことができない。
直線も人間の心の中にある象徴概念の1つ
直線は「ひとつの次元」しかないですよね。
直線の構成を考えてみると
「連続する無数の点」の存在が見えてきます。
無数の点に「連続性」という法則性・性質・関係性が生まれた。
直線によって表されているのは
<絶対なるもの>によって作られた
無数に多くの対立する二者という神聖さ
BBA目線:2つの点から「有限」と「無限」が生まれた!
上の小難しい「象徴概念」よりも
BBAが「はっ」としたのは
2つの点=そこには関係性がある
その2つの点から図を創造する時
⇓


「有限」と「無限」が姿を見せた!
ここに、「あ”-!」ってなりました。
単純にベイマックスに見えなくもない(・-・)
ディズニームービーブック ベイマックス (ディズニーストーリーブック)
んで、無知な私でも感じたこの「あ”-!」って気づきつーか感覚
これが「2」のとても重要な部分なのです。
つづく。



